SOM Visualization Guide

This comprehensive guide covers all visualization capabilities available in TorchSOM for analyzing and interpreting Self-Organizing Maps effectively.

Overview

TorchSOM provides a rich set of visualization tools through the SOMVisualizer class, supporting both rectangular and hexagonal topologies. All visualizations are designed to help you understand:

Training Progress: How well your SOM is learning over time
Data Distribution: How input data maps onto the SOM grid
Topology Preservation: Whether neighborhood relationships are maintained
Feature Representation: How individual features are distributed across neurons
Cluster Structure: Identification of natural groupings in your data

Quick Start

Basic Visualization Setup

from torchsom import SOM
from torchsom.visualization import SOMVisualizer, VisualizationConfig
import torch

# Train a SOM
data = torch.randn(1000, 4)
som = SOM(x=20, y=15, num_features=4, epochs=50)
som.initialize_weights(data=data, mode="pca")
q_errors, t_errors = som.fit(data)

# Create visualizer with default configuration
visualizer = SOMVisualizer(som=som)

# Generate all visualizations at once
visualizer.plot_all(
    quantization_errors=q_errors,
    topographic_errors=t_errors,
    data=data,
    save_path="som_results"
)

Custom Configuration

The VisualizationConfig class provides comprehensive customization options:

config = VisualizationConfig(
    figsize=(12, 8),                    # Figure size in inches
    fontsize={                          # Font sizes for different elements
        "title": 16,
        "axis": 13,
        "legend": 11
    },
    fontweight={                        # Font weights
        "title": "bold",
        "axis": "normal"
    },
    cmap="viridis",                     # Default colormap
    dpi=150,                            # Resolution for saved figures
    grid_alpha=0.3,                     # Grid transparency
    colorbar_pad=0.01,                  # Colorbar padding
    save_format="png",                  # Save format (png, pdf, eps, svg)
    hexgrid_size=None                   # Hexagonal grid size (auto if None)
)

Visualization Types

Training Errors

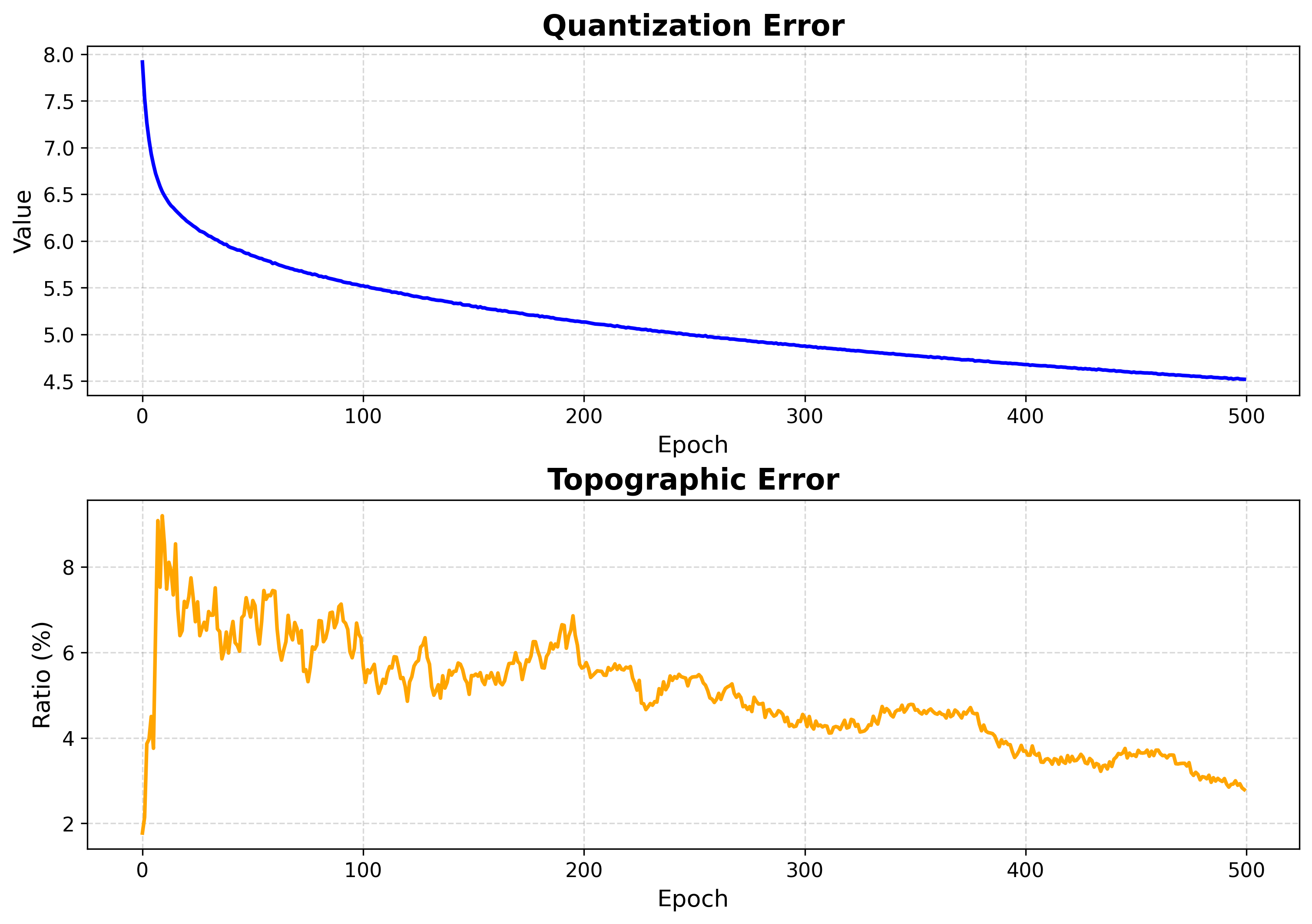
Monitors SOM learning progress by plotting quantization and topographic errors over epochs.

visualizer.plot_training_errors(
    quantization_errors=q_errors,
    topographic_errors=t_errors,
    save_path="results"
)

Interpretation:

Quantization Error: Measures how well the SOM represents the input data (lower is better)
Topographic Error: Measures topology preservation (lower percentage is better)
Convergence: Both errors should generally decrease and stabilize during training

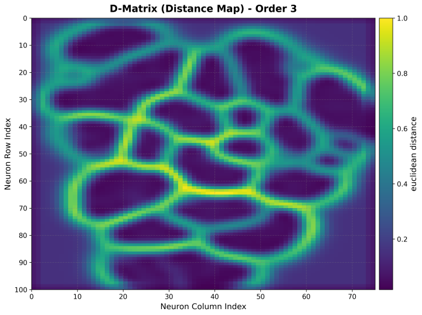
Distance Map (U-Matrix)

The unified distance matrix shows the distance between each neuron and its neighbors, revealing cluster boundaries.

visualizer.plot_distance_map(
    save_path=save_path
    distance_metric=som.distance_fn_name,
    neighborhood_order=som.neighborhood_order,
    scaling="sum",
)

Interpretation:

Dark Regions: Small distances between neighboring neurons (cluster boundaries)
Light Regions: Large distances between neighboring neurons (within clusters)
Topology: Works with both rectangular and hexagonal grids

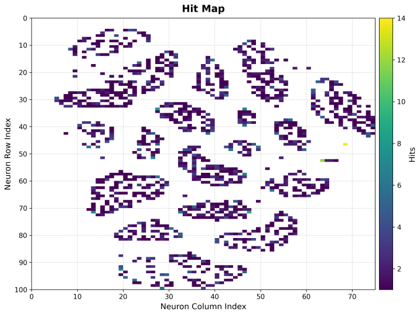
Hit Map

Shows the frequency of neuron activation, indicating how often each neuron was selected as the Best Matching Unit (BMU).

visualizer.plot_hit_map(
    data=train_features,
    save_path=save_path,
    batch_size=train_features.shape[0],
)

Interpretation:

Bright Areas: Frequently activated neurons (high data density)
Dark Areas: Rarely activated neurons (low data density or dead neurons)
Usage: Identifies data distribution patterns and potential dead neurons

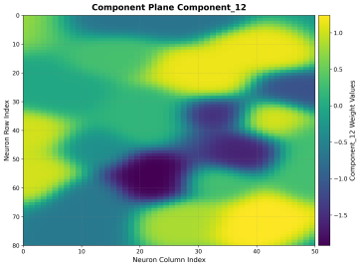
Component Planes

Individual visualizations for each input feature dimension, showing how feature weights are distributed across the map.

visualizer.plot_component_planes(
    component_names=feature_names,
    save_path=save_path
)

Interpretation:

One Plane per Feature: Shows weight values for each input dimension
Pattern Analysis: Reveals feature level in different map regions

Supervised Maps

Visualizations for supervised learning tasks, including both classification and regression, help interpret how target information is distributed across the SOM map.

Classification Case

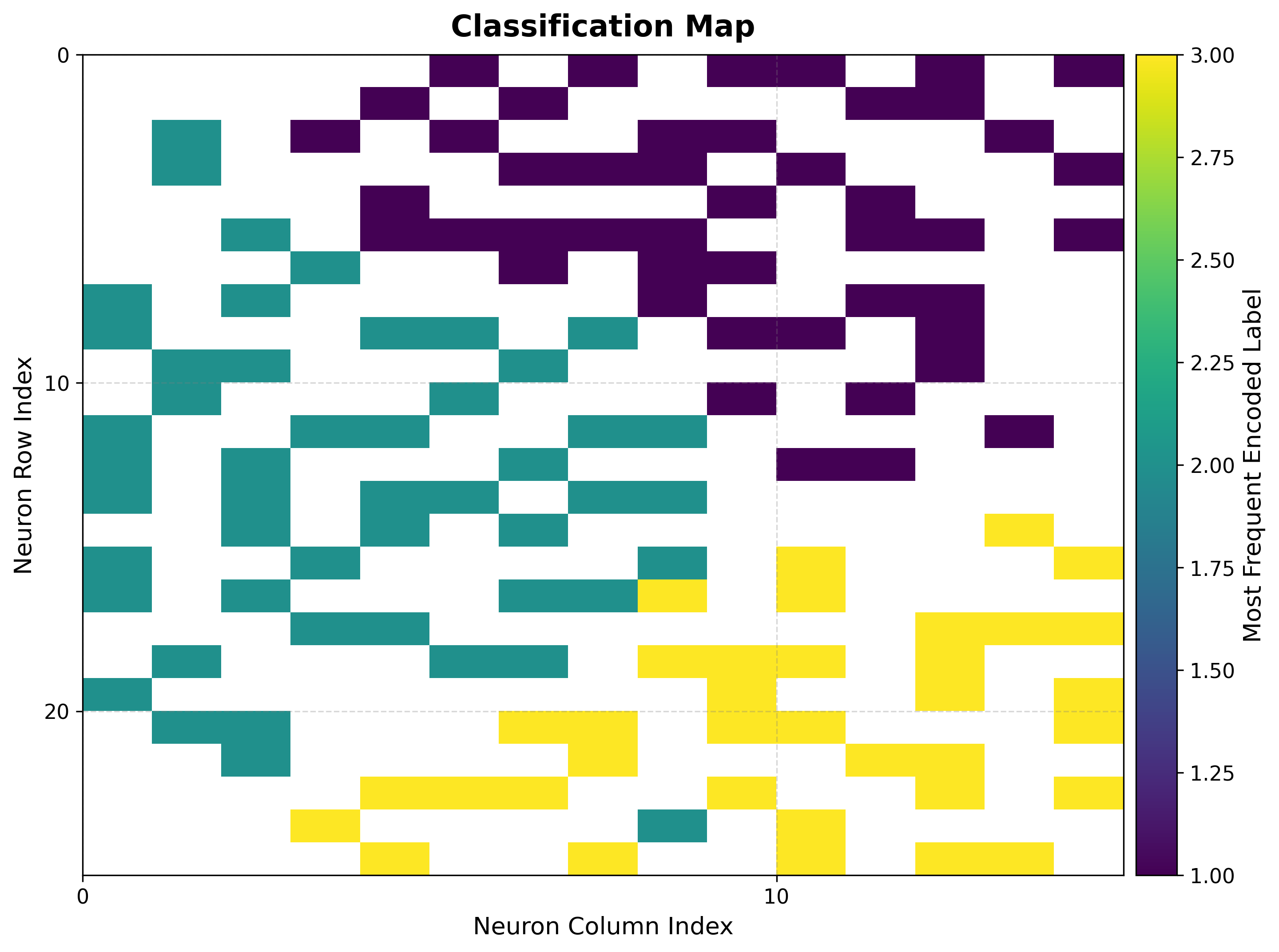
Displays the most frequent class label assigned to each neuron, providing insight into class separation and cluster structure.

visualizer.plot_classification_map(
    data=train_features,
    target=train_targets,
    save_path=save_path,
    bmus_data_map=bmus_map,
    neighborhood_order=som.neighborhood_order,
)

Interpretation:

Color Coding: Each color represents a different class label.
Cluster Identification: Reveals spatial organization of classes on the map.
Decision Boundaries: Boundaries between colors indicate class separation.

Regression Case

Analyzes the distribution of continuous target values (e.g., for regression tasks) using statistical summaries per neuron.

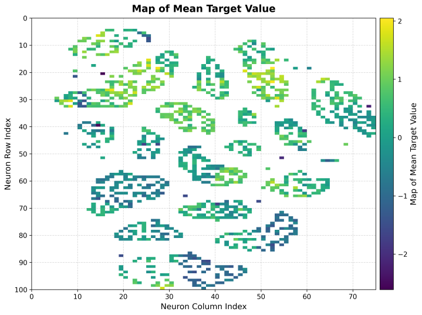
Mean Map

Shows the average target value for samples mapped to each neuron.

visualizer.plot_metric_map(
    data=train_features,
    target=train_targets,
    reduction_parameter="mean",
    save_path=save_path,
    bmus_data_map=bmus_map,
)

Interpretation:

Color Scale: Indicates the mean target value per neuron.
Smooth Transitions: Suggest good topology preservation.
Hot Spots: Highlight neurons with extreme target values.

Standard Deviation Map

Shows the variability of target values for each neuron, useful for assessing prediction reliability.

visualizer.plot_metric_map(
    data=train_features,
    target=train_targets,
    reduction_parameter="std",
    save_path=save_path,
    bmus_data_map=bmus_map,
)

Interpretation:

Low Values: Neurons with consistent (low-variance) target values—good for prediction.
High Values: Neurons with variable (high-variance) target values—less reliable.
Quality Assessment: Helps identify the most reliable neurons for regression tasks.

Advanced Visualizations

Score Map

Evaluates neuron representativeness using a composite score combining standard error and sample distribution.

visualizer.plot_score_map(
    bmus_data_map=bmus_map,
    target=train_targets,
    total_samples=train_features.shape[0],
    save_path=save_path,
)

\[S_{ij} = \frac{\sigma_{ij}}{\sqrt{n_{ij}}} \cdot \log\left(\frac{N}{n_{ij}}\right)\]

where:

\(S_{ij} \in \mathbb{R}^+\): Reliability score of neuron at position \((i, j)\)

\(\sigma_{ij} \in \mathbb{R}^+\): Standard deviation of target values assigned to neuron at position \((i, j)\)

\(n_{ij} \in \mathbb{N}\): Number of samples assigned to neuron at position \((i, j)\)

\(N \in \mathbb{N}\): Total number of samples in the latent space

Interpretation:

Lower Scores: Better neuron representativeness
Usage: Identifies most reliable neurons for analysis

Rank Map

Ranks neurons based on their target value standard deviations.

visualizer.plot_rank_map(
    bmus_data_map=bmus_map,
    target=train_targets,
    save_path=save_path,
)

Interpretation:

Rank 1: Lowest standard deviation (best predictive neurons)
Higher Ranks: Increasing standard deviation
Selection: Use top-ranked neurons for reliable predictions

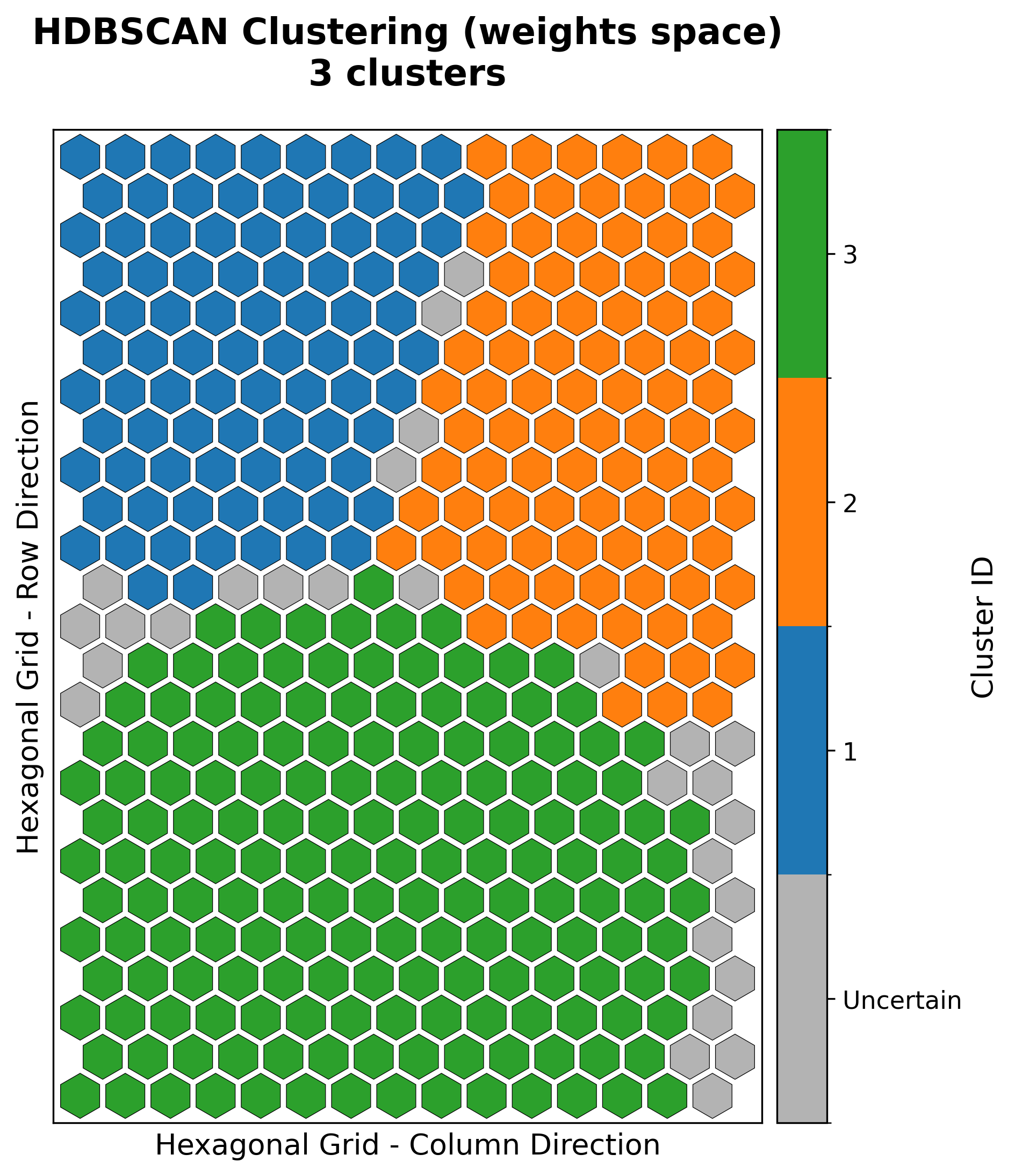
Cluster Map

Clusters neurons based on algorithms like HDBSCAN, KMeans, or GMMs.

cluster = som.cluster(
   method="hdbscan", # hdbscan, kmeans, gmm
   n_clusters=n_clusters,
   feature_space="weights",
)

visualizer.plot_cluster_map(
    cluster_result=cluster,
    save_path=save_path,
)

Troubleshooting

White Cells in Visualizations:

Indicates neurons with zero values or NaN
Check for dead neurons in hit map
Verify data preprocessing and normalization

Memory Issues:

Reduce batch size in visualization functions
Use CPU-only mode for very large SOMs
Clear GPU cache with torch.cuda.empty_cache()

Topology Preservation:

High topographic error indicates poor topology preservation
Consider adjusting learning rate, sigma, or training epochs
Use PCA initialization for better convergence

References

For more examples and detailed usage, see: