Basic Concepts
This page introduces the fundamental concepts behind Self-Organizing Maps (SOMs) and how they work.
What is a Self-Organizing Map?
A Self-Organizing Map (SOM), also known as a Kohonen map, is an unsupervised neural network algorithm that:
Clusters similar data points together
Reduces dimensionality by mapping high-dimensional data to a lower-dimensional grid, usually 2D
Preserves topology by keeping similar data points close together on the map
Visualizes patterns in complex, high-dimensional datasets
Key Characteristics:
Unsupervised: No labeled data required
Competitive learning: Neurons compete to represent input data
Topology preservation: Maintains neighborhood relationships
Dimensionality reduction: Maps N-dimensional data to 2D grid
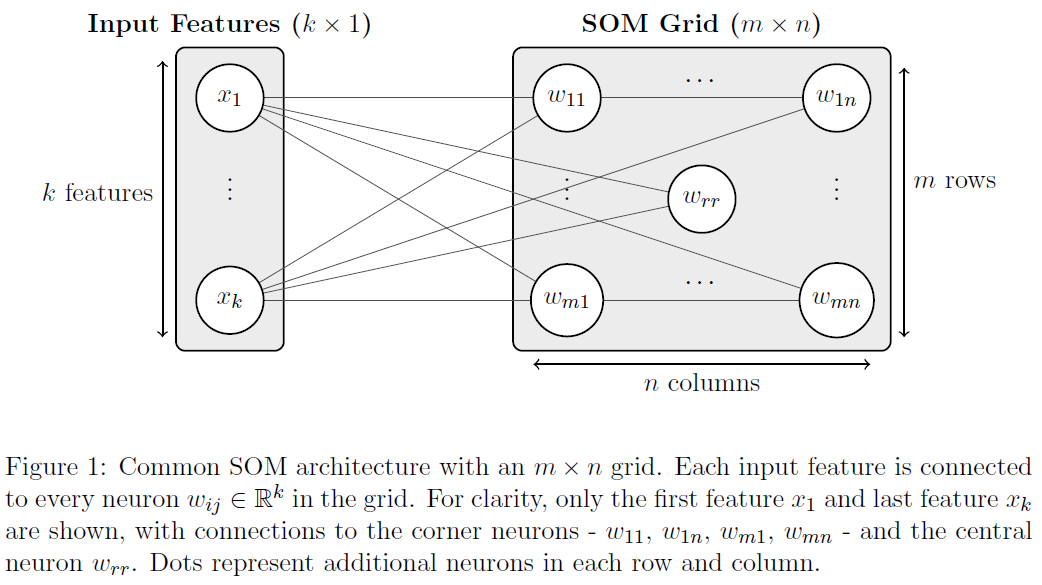
How SOMs Work
The SOM Algorithm
Initialize weight vectors randomly for each neuron
Present input data to the network
Find the Best Matching Unit (BMU) - the neuron most similar to input
Update the BMU and its neighbors to be more similar to the input
Repeat until convergence or maximum iterations reached
Mathematical Foundation
Distance Calculation The similarity between an input vector \(\mathbf{x}\) and a neuron’s weight vector \(\mathbf{w}\) is most commonly measured using the Euclidean distance. Alternative distance functions are also supported; see 4. Distance Functions for a comprehensive list.
Weight Update Rule The weights of the neurons are updated according to the following rule:
where:
\(\mathbf{w}_{ij}(t) \in \mathbb{R}^k\): weight vector of the neuron at row \(i\), column \(j\) at iteration \(t\)
\(\alpha(t) \in \mathbb{R}\): learning rate at iteration \(t\)
\(h_{ij}(t) \in \mathbb{R}\): neighborhood function value for neuron \((i, j)\) at iteration \(t\)
\(\mathbf{x} \in \mathbb{R}^k\): input feature vector
Core Components
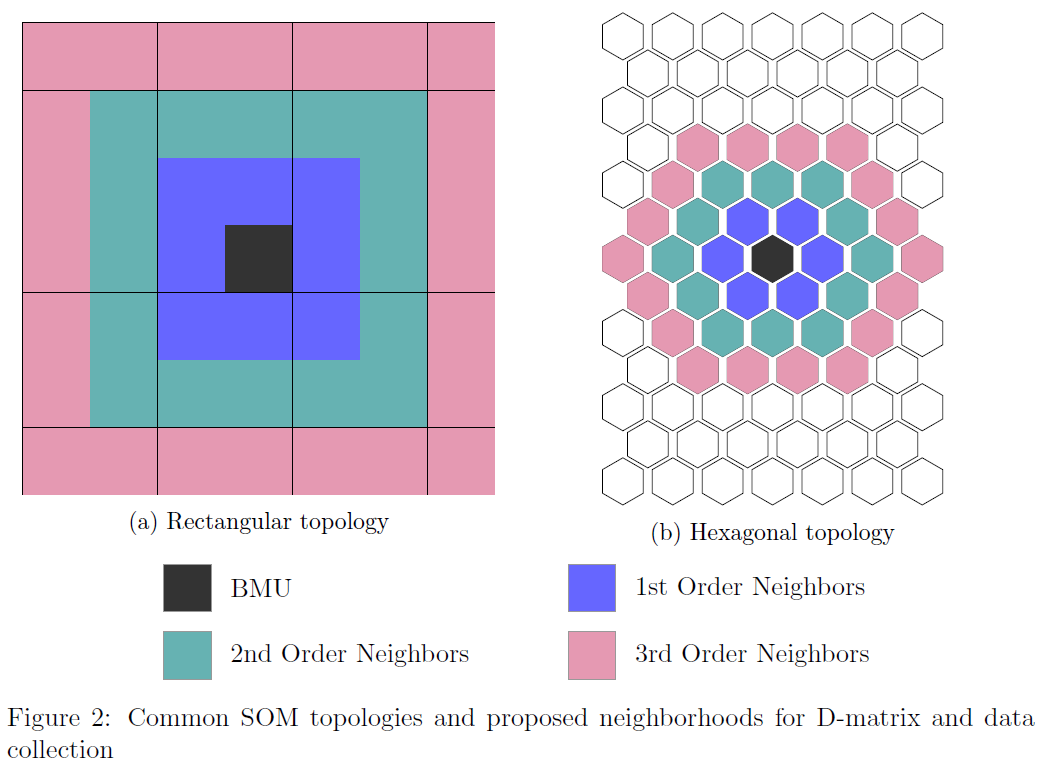
1. Grid Topology
SOMs arrange neurons in a regular grid structure, which determines the map’s topology and neighborhood relationships:
- Rectangular Grid
Simple, intuitive visualization
Suitable for most applications
- Hexagonal Grid
Uniform neighborhood distances
Reduces topology errors, often preferred for advanced analysis
2. Neighborhood Function
The neighborhood function determines how much each neuron is influenced by the BMU during weight updates:
- Gaussian (most common):
- \[h_{ij}^{\mathrm{Gaussian}}(t) = \exp\left(-\frac{d_{ij}^2}{2\,\sigma(t)^2}\right)\]
- Mexican Hat:
- \[h_{ij}^{\mathrm{Mexican}}(t) = \frac{1}{\pi\,\sigma(t)^4} \left(1 - \frac{d_{ij}^2}{2\,\sigma(t)^2}\right) \exp\left(-\frac{d_{ij}^2}{2\,\sigma(t)^2}\right)\]
- Bubble:
- \[\begin{split}h_{ij}^{\mathrm{Bubble}}(t) = \begin{cases} 1, & \text{if } d_{ij} \leq \sigma(t) \\ 0, & \text{otherwise} \end{cases}\end{split}\]
- Triangle:
- \[h_{ij}^{\mathrm{Triangle}}(t) = \max\left(0,\, 1 - \frac{d_{ij}}{\sigma(t)}\right)\]
When updating neuron weights, the distance \(d_{ij}\) is computed in the grid (map) space, not in the input feature space:
where:
\((c_x, c_y)\): coordinates of the BMU in the grid
\((i, j)\): coordinates of neuron \(w_{ij}\)
3. Schedule Learning Rate and Neighborhood Radius Decay
Learning Rate Decay
The learning rate \(\alpha(t)\) controls the magnitude of weight vector updates during training, directly influencing convergence speed and final map quality.
- Inverse Decay:
- \[\alpha(t+1) = \alpha(t) \cdot \frac{\gamma}{\gamma + t} % , \quad \text{where } \gamma = \frac{T}{100}\]
- Linear Decay:
- \[\alpha(t+1) = \alpha(t) \cdot \left( 1 - \frac{t}{T} \right)\]
These schedulers guarantee convergence to \(\alpha(T) = 0\), corresponding to zero weight updates in the final training phase, which is essential for achieving precise local weight adjustments.
Neighborhood Radius Decay
The neighborhood radius controls the size of the neighborhood of the BMU during weight updates.
- Inverse Decay:
- \[\sigma(t+1) = \frac{\sigma(t)}{1 + t \cdot \frac{\sigma(t) - 1}{T}}\]
- Linear Decay:
- \[\sigma(t+1) = \sigma(t) + t \cdot \frac{1 - \sigma(t)}{T}\]
These schedulers guarantee convergence to \(\sigma(T) = 1\), corresponding to single-neuron updates in the final training phase, which is essential for achieving precise local weight adjustments.
Asymptotic Decay
For arbitrary dynamic parameters requiring exponential-like decay characteristics, TorchSOM implements a general asymptotic decay scheduler:
where:
\(\alpha(t) \in \mathbb{R}^+\): learning rate at iteration \(t\)
\(\sigma(t) \in \mathbb{R}^+\): neighborhood function width at iteration \(t\)
\(\theta(t) \in \mathbb{R}^+\): general dynamic parameter at iteration \(t\)
\(T \in \mathbb{N}\): total number of training iterations
\(t \in \{0, 1, \ldots, T\}\): current iteration index
\(\gamma \in \mathbb{R}^+\): inverse decay rate parameter, typically \(\gamma = T/100\)
4. Distance Functions
Different ways to measure similarity:
- Euclidean:
- \[d_{\text{Euclidean}}(x, w_{ij}) = \sqrt{\sum_{l=1}^k {(x_l - w_{ij,l})}^2}\]
- Cosine:
- \[d_{\text{cosine}}(x, w_{ij}) = 1 - \frac{x \cdot w_{ij}}{\|x\| \|w_{ij}\|}\]
- Manhattan:
- \[d_{\text{Manhattan}}(x, w_{ij}) = \sum_{l=1}^k |x_l - w_{ij,l}|\]
- Chebyshev:
- \[d_{\text{Chebyshev}}(x, w_{ij}) = \max_{l} |x_l - w_{ij,l}|\]
- where:
\(x \in \mathbb{R}^k\): input feature vector
\(w_{ij} \in \mathbb{R}^k\): weight vector of the neuron at row \(i\), column \(j\)
\(k \in \mathbb{N}\): number of features
\(l \in \{1, \ldots, k\}\): feature index
5. Quality Metrics
Quantization Error Average distance between data points and their BMUs. Lower is better, measures how well the map represents the data.
Quantization Error
Average distance between data points and their BMUs. Lower is better; measures how well the map represents the data.
Topographic Error
Percentage of data points whose BMU and second-BMU are not neighbors. Lower is better; measures topology preservation.
where:
\(N \in \mathbb{N}\): Number of training samples
\(x_i \in \mathbb{R}^k\): The \(i\)-th input training sample
\(w_{\text{BMU}}(x_i) \in \mathbb{R}^k\): Weight vector of the Best Matching Unit (BMU) for input \(x_i\)
\(w_{\text{2nd-BMU}}(x_i) \in \mathbb{R}^k\): Weight vector of the second BMU for input \(x_i\)
\(d_{\text{th}} \in \mathbb{R}^+\): Threshold distance for topological adjacency (typically \(d_{\text{th}} = 1\))
\(\mathbb{I}(\cdot) \in \{0, 1\}\): Indicator function
\(\| \cdot \|_2\): Euclidean norm in feature space
\(d_{\text{grid}}(\cdot, \cdot)\): Grid space distance between BMUs of input \(x_i\)
Strengths and Weaknesses
Advantages
No assumptions about data distribution
Topology preservation maintains relationships
Intuitive visualization of complex data
Unsupervised learning - no labels needed
Limitations
Calculations can be expensive for large datasets
Parameter selection is important - requires tuning
Interpretation challenges for very high dimensions
Best Practices
Data Preparation
Normalize features to similar scales
Remove highly correlated features
Handle missing values appropriately
Consider dimensionality reduction for very high dimensions
Parameter Selection
Experiment with different topologies and functions
Monitor training progress with error curves to guide parameter choice
Interpretation
Use multiple visualizations to understand the map
Combine with domain knowledge for meaningful insights
Validate findings with other analysis methods
Document parameter choices for reproducibility
Next Steps
Now that you understand the basics, explore:
SOM Visualization Guide - Visualization techniques